Convex Optimization,凸优化
1. 几个基本概念
1.1. 凸集
如果集合\(C\)中任意两点间的线段仍然在\(C\)中,即满足: \[\left. \begin{aligned} \forall x_1, x_2 \in C & \\ \forall\ \theta\ ,\ 0 \leqslant \theta \leqslant 1 & \end{aligned} \right\} \Longrightarrow \theta x_1 + (1-\theta)x_2 \in C \]
多点推广: \[\left. \begin{aligned} \forall x_1, x_2, \ldots, x_k \in C & \\ \theta_i \geqslant 0, \ i = 1, \ldots, k & \\ \sum_{i=1}^k \theta_i = 1 & \end{aligned} \right\} \Longrightarrow \theta_i x_i + \ldots + \theta_k x_k \in C \]
多点推广的证明: 1, 三点成立证明 \[\begin{aligned} \left. \begin{aligned} \left. \begin{aligned} \left. \begin{aligned} \forall x_1, x_2 \in C & \\ \forall\ \theta_1\ ,\ 0 \leqslant \theta_1 \leqslant 1 & \end{aligned} \right\} \Longrightarrow \theta_1 x_1 + (1-\theta_1)x_2 \in C \\ \forall\ \theta_2\ ,\ 0 \leqslant \theta_2 \leqslant 1 \\\ \forall\ x_3 \in C \\ \end{aligned} \right\} \Longrightarrow \theta_2 (\theta_1 x_1 + (1-\theta_1)x_2) + (1-\theta_2)x_3 \in C \\ \left. \begin{aligned} &0 \leqslant \theta_1, \theta_2, \theta_3 \leqslant 1 \\ set:\ &\theta_1'=\theta_2 \theta_1 \\ &\theta_2'=\theta_2(1-\theta_1) \\ &\theta_3'=(1-\theta_2) \end{aligned} \right\} \Longrightarrow \left\{ \begin{aligned} \theta_1' + \theta_2' + \theta_3' = 1 \\ 0 \leqslant \theta_1',\theta_2', \theta_3' \leqslant 1 & \end{aligned} \right. \end{aligned} \right\} &\\ \\ \Longrightarrow \theta_1' x_1 + \theta_2' x_2 + \theta_3' x_3 \in C & \end{aligned} \]
整理上式得: \[\left. \begin{aligned} \forall \ x_1, x_2, x_3 \in C & \\ \forall \ \theta_i, 0 \leqslant \theta_i \leqslant 1 & \ \ i \in [1, 3]\\ \theta_1' + \theta_2' + \theta_3' = 1& \end{aligned} \right\} \Longrightarrow \theta_1' x_1 + \theta_2' x_2 + \theta_3' x_3 \in C \]
2, k点成立正证明: 用同样的方法可以证明k-1个点到k个点的情况, 即通过归纳法证得多点也成立
1.2. 仿射集
如果集合\(C\)中任意两点决定的直线仍然在\(C\)中, 即满足: \[\left. \begin{aligned} \forall x_1, x_2 \in C & \\ \forall\ \theta\ & \end{aligned} \right\} \Longrightarrow \theta x_i + (1-\theta)x_2 \in C \] 类似凸集可推广到多点
凸集是仿射集的真子集
1.3. 凸函数
如果函数\(\ f\ \)定义域是凸集,对于定义域内的任意\(\ x, y \in \boldsymbol{dom}\ f\ \) 和任意\(\ 0 \leqslant \theta \leqslant 1\ \), 有 \(f\big(\theta x + (1-\theta)y\big) \leqslant \theta f(x) + (1-\theta)f(y)\), 即:
\[\left. \begin{aligned} \ 函数f\ 的定义域\boldsymbol{dom}\ f\ 是凸集 & \\ \ \forall x, y \in \boldsymbol{dom}\ f\ & \\ \forall \theta\ ,\ 0 \leqslant \theta \leqslant 1 & \end{aligned} \right\} \Longrightarrow f(\theta x + (1-\theta)y) \leqslant \theta f(x) + (1-\theta)f(y) \]
- 即,定义域内,两点的期望的函数值小于分别求函数值的期望, 亦即\(\ f(E(x)) \leqslant E(f(x))\)
- 当以上不等式存在’\(=\)’成立时,是非严格凸, 否则为严格凸
1.3.1. 凸函数的判断
1.3.1.1. 根据定义判断
直接利用定义证明
1.3.1.2. 一阶条件判断
假设函数\(\ f\ \)可微, 则: \[f是凸函数 \Longleftrightarrow \left\{ \begin{aligned} & \boldsymbol{dom} \ f\ 是凸集 \\ & \forall \ x, y \in \boldsymbol{dom}\ f \\ & f(y) \geqslant f(x) + \nabla f(x)^\mathsf{T}(y-x) \ \ \ \ \ (任意点的函数值大于等于任意切线在该点的值) \end{aligned} \right. \]
1.3.1.3. 二阶条件判断
如果函数\(\ f \ \)二阶可微, 则\(\ f \ \)为凸函数的充要条件是, 二阶导数\(Hessian\)矩阵是正定阵
1.4. 仿射函数
如果具有 \(f(x)\ =\ \boldsymbol{A}\boldsymbol{x}+\boldsymbol{b}\)的形式的函数\(\ f\ \)称为仿射函数
- 凸函数是仿射函数的真子集
2. 优化与凸优化问题表示
2.1. 优化问题的一般形式
\[\begin{aligned} obj\ :&\ \ \min\ f_0(x) \\ st\ :&\ \ f_i(x) \leqslant 0, \ i = 1,2, \ldots, m \ \\ &\ \ h_i(x) = 0, i = 1, 2, \ldots, p \end{aligned} \]
2.2. 凸优化问题的一般形式
\[\begin{aligned} obj\ :&\ \ \min\ f_0(x) & \\ st\ :&\ \ f_i(x) \leqslant 0\ , \ i = 1,2, \ldots, m &\\ &\ \ h_i(x) = 0, i = 1, 2, \ldots, p & \\ &\ \ f_0(x)\ 是凸函数 \\ &\ \ f_i(x)\ 是凸函数,\ i \in [1, m] & \\ &\ \ h_i(x)\ 是仿射函数, 即h_i(x)为\boldsymbol{A}\boldsymbol{x}+\boldsymbol{b} 的形式\ , i \in [1, p] & \end{aligned} \]
3. 拉格朗日乘子法
3.1. 广义拉格朗日函数:
\[\begin{aligned} & L(x, \boldsymbol{\lambda}, \boldsymbol{\nu}) = f_0(x) + \sum_{i=1}^m\lambda_i f_i(x) + \sum_{i=1}^p \nu_i h_i(x) \\ & \boldsymbol{\nu} \in \boldsymbol{R}^p , \ \boldsymbol{\lambda} \in \boldsymbol{R}^m \\ & \lambda_i \geqslant 0, \ i \in [1, m] \end{aligned}\]
3.2. 拉格朗日函数:
\[\theta_p(x) = \max_{\boldsymbol{\lambda}, \boldsymbol{\nu}}{L(x, \boldsymbol{\lambda}, \boldsymbol{\nu})} \left\{ \begin{aligned} f_0(x), & \ \ x满足原始问题的约束 \\ +\infty, & \ \ 其他\\ \end{aligned} \right. \]
3.3. 拉格朗日函数的理解
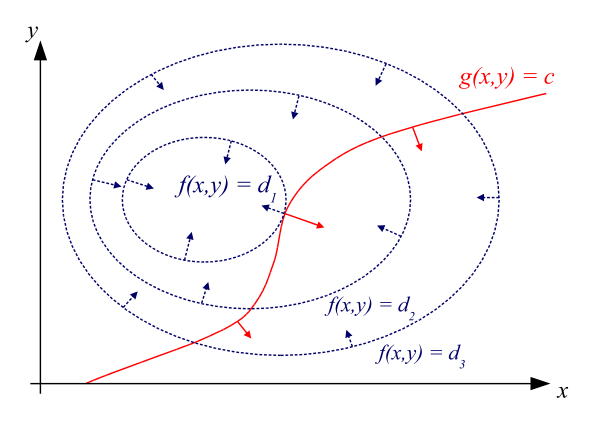
当\(g(x, y) - c = 0\)时红色线表示等式约束;
当\(g(x, y) - c \leqslant 0\) 红色线箭头方向为不等式约束成立的方向)
- 等高线: 考虑三维情况, \(z=f_0(x, y)\)的情况,等高面\(z = d\)与函数\(f_0(x, y)\)相交的部分为等高线, 等高线在\((x, y)\)平面的投影可表示为\(f_0(x, y)=d\)
3.3.1. 一个等式的约束问题
如图假设等式约束为 \(h_1(x, y)=g(x, y) - c=0\), 拉格朗日函数表示为: \(L=f_0(x, y) + \nu h_1(x, y)\). 如果函数\(f_0(x, y)\) 的值域连续, 则其等高线投影与\(g(x, y) -c\)相切处取得等式约束条件下的极值,此时\(f_0(x, y)\)
\[\left.
\begin{aligned}
& \left.
\begin{aligned}
f_0(x, y)与h_1(x, y)相切\Rightarrow \nabla_{x, y} f_0(x, y) = \nu' (\nabla_{x, y} h_1(x, y)) \Rightarrow \nabla_{x, y}[f_0 + \nu(h_1)] =0 & \\
h_1(x,y)=0 \Rightarrow \nabla_{\nu}[f_0 + \nu(h_1)] = 0 &
\end{aligned}
\right\} \\
\\
& \Longrightarrow \nabla_{x, y, \nu} \big[f_0(x) + \nu h_1(x) \big] = 0
\\
& \Longrightarrow 目标函数f(x,y)在一个等式约束条件下取得最值处的解与L=f_(x, y) + \nu h_1(x,y)极值的解等价
\end{aligned}
\right.
\]
- 注: \(\nu'\) 可以看作是两个等价切线(超平面)的系数, 同分割超平面的等价超平面的系数\(k\) \(\nu = -\nu'\)
3.3.2. 多个等式约束问题
多个等式约束看作在满足约束条件下集合处, 定义极值处的梯度方向为多个约束加权后得到的梯度和目标函数\(f_0(极点)\)处的梯度平行 即极值处满足: \[\left. \begin{aligned} & \nabla_{\boldsymbol{x}} f(x) = \sum_{i=1}^p \lambda_i' \nabla_{\boldsymbol{\boldsymbol{x}}} f_i(\boldsymbol{x}) \\ & f_i(x) = 0, \ \ i = 1,\ldots, m \end{aligned} \right\} \Longrightarrow \nabla_{\boldsymbol{x}, \boldsymbol{\lambda}} \big[f_0(x) + \sum_{i=1}^p \lambda_i f_i(x)\big] = 0, \ \ \ \ 当\lambda_i \neq 0时, \ \ i = 1,\ldots, m \]
3.3.3. 一个不等式等式约束
假设目标函数\(\min f_0(x)\), 有不等式约束\(f_1(x) < 0\) 如图1表示, 当不等式约束有效时,须使得目标函数的函数值减小的方向与不等式约束成立的方向相反且目标函数与不等式约束的边界相切时取得极值. 即如果约束有效的情况下, 目标函数取得极值时一定在约束的边界处, 问题可以简化为等式约束的情况
边界有效时: 目标函数的函数值减小的方向与不等式约束成立的方向相反 则: \[\left. \begin{aligned} f_0(x)降低方向的梯度为: -\nabla f_0(x) & \\ f_1(x) < 0所表示定义域方向梯度方向为: -\nabla f_1(x) & \\ f_0(x)与f_1(x)相切,且降低方向的梯度和定义域方向梯度相反 & \end{aligned} \right\} \Longrightarrow \left\{ \begin{aligned} & \nabla f_0(x) = -\lambda \nabla f_1(x) \\ & \lambda > 0 \end{aligned} \right. \]
考虑不等式约束无效的情况, 目标函数降低方向的梯度和定义域方向梯度相同, 即假设不等式约束成立的方向为图1中红色箭头相反的方向, 此时仍然可以有目标函数与不等式约束边界相切, 但是所求\(\lambda < 0\), 且此时切点对应的函数值显然不是极值处
另外,只考虑不等式约束时, 不等式自身约束恒成立力时(或着当有多个约束时, 其他约束的定义域为该约束的子集. 即该约束对所有约束的交集无贡献), 该约束项的乘子可为0.
综上: 考虑约束的有效性综, 不等式约束的朗格朗日乘\(\lambda \leqslant 0\), 等号拉格朗日乘子等于0时,代表约束对取得最值时无贡献
3.3.4. 多个不等式约束
多个不等式约束同多个不等式约束的情况. 其中每个不等式约束的朗格朗日乘子均大于等于0
3.3.5. 多个等式约束和多个不等式约束的情况
同多个等式约束情况, 取得极值处可看作是在可行域内有效约束内且由权值为拉格朗日乘子加权作为梯度平行于原函数的梯度
3.4. 原问题的拉格朗日函数
\[L_P= \min_{\boldsymbol{x}}\max_{\boldsymbol{\lambda}, \boldsymbol{\nu}} {L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\nu})}\]
3.5. 原问题的拉格朗日对偶函数
对偶函数 \[ 令, g(\boldsymbol{\lambda}, \boldsymbol{\nu}) = \inf_{x \in D} L(\boldsymbol{\lambda}, \boldsymbol{\nu}) = \inf_{x \in D}(f_0(x) + \sum_{i=1}^m\lambda_i f_i(x) + \sum_{i=1}^p \nu_i h_i(x)) \]
\[L_D = \max_{\boldsymbol{\lambda}, \boldsymbol{\nu}}\min_{x} {L(x, \lambda, \nu)} = \max_{\boldsymbol{\lambda}, \boldsymbol{\nu}}g(\boldsymbol{\lambda}, \boldsymbol{\nu}) \]
\(g(\boldsymbol{\lambda}, \boldsymbol{\nu})\)被求极小的部分: 可以看成给定一个\(\boldsymbol{x}\), 有\(常数 + 常数向量1 \cdot \boldsymbol{\lambda} + 常数向量2 \cdot \boldsymbol{\nu}\), 即为关于\({\lambda}, \boldsymbol{\nu})\)仿射的; 考虑极小问题,是由无数个, 确定的\(\boldsymbol{x}\)对应的仿射函数逐点求下界,由仿射函数的下界求交集是凹的. 所以\(g(\boldsymbol{\lambda}, \boldsymbol{\nu})\) 是凹的
3.6. 原问题拉格朗日函数与对偶函数的关系
假设原问题和其对偶问题均有最优值
\[\begin{aligned} & \min_{x} {L(x, \lambda, \nu)} \leqslant L(x, \lambda, \nu) \leqslant \max_{\lambda, \nu} {L(x, \lambda, \nu)} \\ \Longrightarrow \ & \max_{\lambda, \nu}\min_{x} {L(x, \lambda, \nu)} \leqslant L(x, \lambda, \nu) \leqslant \min_{x}\max_{\lambda, \nu} {L(x, \lambda, \nu)} \\ \Longrightarrow \ & L_D \leqslant L_P \end{aligned} \]
当上式子取得等号时, 称为强对偶.
3.7. Slater 准则
用于凸优化问题中,强对偶条件成立是否存在
\[\left. \begin{aligned} 原问题为凸优化问题 & \\ 存在 x \in 约束条件的交集, 使得 f_i(x) < 0, i = 1,\ldots, m & \\ \end{aligned} \right\} \Longrightarrow 该问题的强对偶性可以达到 \]
对于在不等式约束函数为仿射函数的情况,只需要找到的\(x\),满足原不等式即可(满足“\(\leqslant\)”, 而不需要更强的条件“\(<\)”) 整理得: \[\left. \begin{aligned} 原问题为凸优化问题 & \\ 存在 x \in 约束条件的交集且f_i(x)不是仿射的满足f_i(x) < 0, \ i = 1,\ldots, k & \\ \end{aligned} \right\} \Longrightarrow 该问题的强对偶性可以达到 \]
证明见:《凸优化》- 清华出版社 Stephen Boyd 等著, 王书宁等译,\(P_{226} - P_{228}\)
3.8. KKT条件
强对偶成立时,最优解需要满足的条件
令\(x^*\)是原问题的最优解,\((\lambda^*, \nu^*)\)对偶问题的最优解 则, \[ \begin{eqnarray} 原始约束问题的最值=拉格朗日对偶问题的最值 \Rightarrow & \ f_0(x^*) & = & g(\lambda^*, \nu^*) \\ 对偶问题的定义\Rightarrow & & = & \inf_{x}\big(f_0(x) + \sum_{i=1}^m \lambda_i^* f_i(x) + \sum_{i=1}^p \nu^*h_i(x)\big) \\ 任意x的逐点求下解值小于其中一个x的值\Rightarrow & & \leqslant & f_0(x^*) + \sum_{i=1}^m \lambda_i^* f_i(x^*) + \sum_{i=1}^p \nu^*h_i(x^*) \\ 不等式约束项小于等于0,等式约束项等于0 \Rightarrow & & \leqslant & f_0(x^*) \\ \end{eqnarray} \]
由\(A \leqslant B \leqslant A\)形式得, \(B = A\) 即有:
\[ \left. \begin{aligned} \left. \begin{aligned} \left. \begin{aligned} f_0(x^*) + \sum_{i=1}^m \lambda_i^* f_i(x^*) + \sum_{i=1}^p \nu_i^*h_i(x^*) = f_0(x^*) \\ 优化问题不等式约束,f_i(x) \leqslant 0 \\ 优化问题的等式约束, h_i(x) = 0 \\ \lambda_i \geqslant 0 \end{aligned} \right\} \Longrightarrow \lambda_i^*f_i(x^*) = 0, i = 1,2, \ldots, m \ \ \ \ & \\ f_i(x) \leqslant 0, i = 1,2, \ldots, p \ \ \ \ & \\ h_i(x) = 0, i = 1,2, \ldots, p \ \ \ \ & \\ \lambda_i \geqslant 0, i = 1,2, \ldots, m \ \ \ \ & \\ 拉格朗日函数在x^*处取得极小值: \nabla_{\boldsymbol{x}} \big[f_0(x) + \sum_{i=1}^m \lambda_i^* f_i(x) + \sum_{i=1}^m \nu_i^*h_i(x) \big]_{x=x^*} = 0 \ \ \ \ & \end{aligned} \right\} KKT条件 \end{aligned} \right. \]
其中 \(\lambda_i^*f_i(x^*)\)为松弛条件 有: \[\left\{ \begin{aligned} & 当 f_i(x) < 0时, \lambda_i = 0. \ 该约束条件为非边界条件,不影响极值 \\ & 当 f_i(x) = 0时, \lambda_i > 0. \ 该约束条件为边界条件,在SVM中该点为支撑向量 \end{aligned} \right. \]
对于非凸问题, 拉格朗日函数的极值未必是原问题的最值, 所以未必是最优解。 对于凸的问题, 满足KKT条件即为原始约束问题的最优解, KKT条件是最优性充要条件
4. …
待续…
5. 参考资料
[1] 《凸优化》,清华出版社 Stephen Boyd,Lieven Vandenberghe著, 王书宁等译
[2] 维基百科-Lagrange multiplier https://en.wikipedia.org/wiki/Lagrange_multiplier
[3] 维基百科-拉格朗日乘数 https://zh.wikipedia.org/wiki/拉格朗日乘数
[4]《统计学习方法》,李航著