SVM,Support Vector Mechines,支持向量机
1. 线性可分SVM
1.1. 问题引出
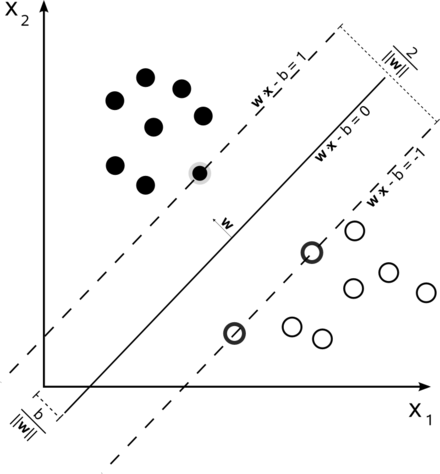
有样本集 \(D=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),\ldots,(\boldsymbol{x_m},y_m)\}\)。其中, \(\boldsymbol{x_i}\)是一个样本,列向量;标签\(y_i\in\{-1, 1\}\)且\(D\)是线性可分的。 找到一个最优超平面\(\boldsymbol{w}^T\boldsymbol{x} + b = 0\)(\(\boldsymbol{w}\)为是超平面系数,列向量;\(b\)为截距;\(\boldsymbol{x}\)为列向量),使得在保证正确分类的情况下,样本点到超平面的最小距离最大化
- 最小距离:所以样本点到超平面的距离
- 支持向量:每个类别中到超平面距离最小的点
- 最大化:使得两类支持向量到超平面最小距离最大化,即两类支持向量点到超平面的距离相等
如上图: \(\boldsymbol{w}^T\boldsymbol{x} + b = 0\): 分离超平面 \(\boldsymbol{w}^T\boldsymbol{x} + b = 1\): 正例支撑超平面 \(\boldsymbol{w}^T\boldsymbol{x} + b = -1\): 负例支撑超平面
1.2. 问题的数学表达
\[假设条件(正确分类条件)\left\{ \begin{aligned} \frac{\boldsymbol{w}^T\boldsymbol{x_i} + b}{\lVert\boldsymbol{w}\rVert} > 0, & \ y_i = +1 \\ \frac{\boldsymbol{w}^T\boldsymbol{x_i} + b}{\lVert\boldsymbol{w}\rVert} < 0, & \ y_i = -1 \\ \end{aligned} \right. \]
\[目标函数与约束条件(最大间隔条件)\left\{ \begin{aligned} obj: & \max_{\boldsymbol{w},b} \frac{\left|\boldsymbol{w}^T\boldsymbol{x_0} + b\right|}{\lVert\boldsymbol{w}\rVert} & & (支撑向量到超平面的距离最大) \\ st: & \frac{\left|\boldsymbol{w}^T\boldsymbol{x_i} + b\right|}{\lVert\boldsymbol{w}\rVert} \geqslant \frac{\left|\boldsymbol{w}^T\boldsymbol{x_0}+ b\right|}{\lVert \boldsymbol{w}\rVert} ,\ i\in[1, m]& & (任意点到对应超平面的距离大于等于支撑向量到超平面的距离) \\ & \boldsymbol{x_0}代表所有支撑向量 & \end{aligned} \right. \]
点到直线的距离: 二维空间中,点\((x_0, y_0)\)到直线\(Ax+By+C=0\)的距离\(d=\frac{\left|Ax_0+By_0+C\right|}{\sqrt{A^{2}+B^{2}}}\). 多纬空间中,点\(\boldsymbol{x_0}\)到\(\boldsymbol{w}^T\boldsymbol{x} + b = 0\)的距离 \(d=\frac{\left| \boldsymbol{w}^T\boldsymbol{x_0} + b \right|}{\lVert \boldsymbol{w} \rVert_2}\)
1,由于\(\lVert\boldsymbol{w}\rVert > 0\), 则假设条件可以写成 \(y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b) > 0\)
2,由于超平面\(\boldsymbol{w}^T \boldsymbol{x} + b = 0\) 有无穷多个等价超平面 \(\kappa(\boldsymbol{w}^T\boldsymbol{x} + b) = 0\), 所以存在等价超平面 \(\boldsymbol{w'}^T\boldsymbol{x} + b' = 0\)使得不在该超平面上的点\(x_0\)满足\(\left|\boldsymbol{w'}^T\boldsymbol{x_0} + b'\right| = 1\)
3,固定点到所有等价超平面的距离相等
基于以上,合并正确分类条件和最大间隔条件
\[\left\{ \begin{aligned} obj: & \max_{\boldsymbol{w'},b'} \frac{1}{\lVert\boldsymbol{w'}\rVert} & \\ st: & y_i(\boldsymbol{w'}^T\boldsymbol{x_i} + b')\geqslant 1,\ i\in[1, m]& \\ & 满足y_0(\boldsymbol{w'}^T\boldsymbol{x_0} + b') = 1 的点为支撑向量& \end{aligned} \right. \]
对上式变量替换及极值等价为以下: \[\left\{ \begin{aligned} obj: & \min_{\boldsymbol{w},b} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 & \\ st: & y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b)\geqslant 1,\ i\in[1, m]& \\ & 满足y_0(\boldsymbol{w}^T\boldsymbol{x_0} + b) = 1 的点为支撑向量& \end{aligned} \right. \]
注:\(\ \)此时所求\(\boldsymbol{w}^T\boldsymbol{x} + b = 0\) 为原始假设超平面的等价超平面
问题目标: 找到满足上是约束的分离超平面参数\(\boldsymbol{w^*}\), \(b^*\),求的分离超平面为\(\boldsymbol{w^*} \cdot \boldsymbol{x} + b^* = 0\), 对于待预测样本\(\boldsymbol{x_i}\)分类决策函数为:\[f(x) = sign(\boldsymbol{w^*} \cdot \boldsymbol{x_i} + b)\]
1.3. 求解
根据凸优化简介,原问题可以写作: \[\left\{ \begin{aligned} obj: & \min_{\boldsymbol{w},b} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 & \\ st: & 1 - y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b)\leqslant 0,\ i\in[1, m]& \end{aligned} \right. \] 由于目标函数是二次函数是凸的,约束函数是关于\(w_i\) 和 \(b\)的仿射函数,所以此问题的为凸优化问题
引入拉格朗日乘子\(\alpha_i, i \in [1, \ldots, m]\), 其拉格朗日函数为 \[L(\boldsymbol{w}, b, \boldsymbol{\alpha}) = \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + \sum_{i=1}^m \alpha_i \big[1 - y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b) \big]\]
1.3.1. 问题的拉格朗日函数
\[\min_{\boldsymbol{w}, b} \max_\boldsymbol{\alpha} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \]
1.3.2. 对偶函数为
\[\max_\boldsymbol{\alpha} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \]
1.3.3. KKT条件
对照凸优化简介,为有若干个不等式约束的凸优化情况 \[\left\{ \begin{aligned} & \nabla_{\boldsymbol{x}} L = 0 & \Longrightarrow & \ \ \left\{ \begin{aligned} & \nabla_{\boldsymbol{w}} L(\boldsymbol{w}, b, \boldsymbol{\alpha})_{\boldsymbol{w}=\boldsymbol{w}^*, b=b^*} = \boldsymbol{0} & \ \ \ \ (1)\\ & \nabla_{b} L(\boldsymbol{w}, b, \boldsymbol{\alpha})_{\boldsymbol{w}=\boldsymbol{w}^*, b=b^*} = 0 & \ \ \ \ (2) \end{aligned} \right. \\ & \lambda_i^*f_i(x^*) = 0 & \Longrightarrow & \ \ \alpha_i^* \big(y_i(\boldsymbol{w}^* \cdot \boldsymbol{x_i} + b^*) -1 \big) = 0 , i = 1, \ldots, m & \ \ \ \ (3)\\ & f_i(x) \leqslant 0 & \Longrightarrow & \ \ 1 - y_i(\boldsymbol{w}^* \cdot \boldsymbol{x_i} + b^*) \leqslant 0, i = 1, \ldots, m & \ \ \ \ (4) \\ & \lambda_i \geqslant 0 & \Longrightarrow & \ \ \alpha_i \geqslant 0, i = 1, \ldots, m & \ \ \ \ (5) \end{aligned} \right. \]
说明:(1),(2)式中,参数\(\boldsymbol{w}, b\)对应凸优化简介中KKT条件的\(\boldsymbol{x}\), 是待求参数。\(y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b)\geqslant 1,\ i\in[1, m]\) 约束中的\(\boldsymbol{x_i}\)和\(y_i\)为一个样本及其对应的类别,为已知常数
1.3.4. \(\min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha})\)的求解
由KKT条件(1)可得: \[\boldsymbol{w^*} - \sum_{i=1}^m \alpha_i y_i \boldsymbol{x_i} = \boldsymbol{0} \Longrightarrow \boldsymbol{w^*} = \sum_{i=1}^m \alpha_i y_i \boldsymbol{x_i} \ \ \ \ (6)\]
由KKT条件(2)可得: \[\sum_{i=1}^m \alpha_i y_i = 0 \ \ \ \ (7)\]
由KKT条件(3),(4),(5)联立可得:
当\(a_i^* > 0\)时,其对应不等式约束为为边界条件,对应样本点为支持向量,有: \[\begin{aligned} & y_j(\boldsymbol{w}^* \cdot \boldsymbol{x_j} + b^*) -1 = 0, i = 1, \ldots, n。\ \ ( 其中n为支撑向量个数) \\ & 将(6)式带入上式,且 1 = y_j \cdot y_j \\ & \therefore b^* = y_j - \sum_{i=i}^m \alpha_i ^ * y_i(\boldsymbol{x_i} \cdot \boldsymbol{x_j}) \end{aligned} \]
当\(a_i^* = 0\)时,其对应的不等式约束\(y_i (\boldsymbol{w^*} \cdot \boldsymbol{x_i} + b^*) -1 < 0, i = 1,\ldots, m\)为非边界条件,该样本不在支撑超平面
\[ \begin{aligned} & \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \\ = & \frac{1}{2}\lVert\boldsymbol{w^*}\rVert^2 + \sum_{i=1}^m \alpha_i \big(1 - y_i(\boldsymbol{w^*} \cdot \boldsymbol{x_i} + b^*)\big) \\ = & \frac{1}{2}\lVert\boldsymbol{w^*} \rVert^2 + \sum_{i=1}^m \alpha_i - \boldsymbol{w^*} \cdot \sum_{i=1}^m \alpha_i y_i \boldsymbol{x_i} - \sum_{i=1}^m \alpha_i y_i b^* \\ \ = & \frac{1}{2}\lVert\boldsymbol{w^*} \rVert^2 + \sum_{i=1}^m \alpha_i - \boldsymbol{w^*} \cdot \boldsymbol{w^*} - \sum_{i=1}^m \alpha_i y_i b^* \ \ \ \because 式(6): \boldsymbol{w^*} = \sum_{i=1}^m \alpha_i y_i \boldsymbol{x_i} \\ = & -\frac{1}{2}\lVert\boldsymbol{w^*} \rVert^2 + \sum_{i=1}^m \alpha_i - b^* \sum_{i=1}^m \alpha_i y_i \\ = & - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_j(\boldsymbol{x_i} \cdot \boldsymbol{x_j}) + \sum_{i=1}^m \alpha_i \ \ \ \ \because 式(6), 式(7): \sum_{i=1}^m \alpha_i y_i = 0 \end{aligned} \]
1.3.5. \(\max_\boldsymbol{\alpha} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha})\) 函数的解
考虑KKT条件中上式仍有约束的条件,有如下: \[ \begin{aligned} & \max_\boldsymbol{\alpha} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \\ = & \left\{ \begin{aligned} obj\ :\ &\max_{\boldsymbol{\alpha}} -\frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_j(\boldsymbol{x_i} \cdot \boldsymbol{x_j}) + \sum_{i=1}^m \alpha_i, \ \ \ \ i,j \in [1,\ldots, m]\\ st\ :\ &\ \sum_{i=1}^m \alpha^* y_i = 0,i \in [1,\ldots, m] \\ &\ \alpha_i \geqslant 0, i \in [1,\ldots, m] \end{aligned} \right. \end{aligned} \]
上式可以通过SMO方法求得
求得\(a_i^*\)后,分离超平面为: \[\sum_{i=1}^m a_i^* y_i(\boldsymbol{x} \cdot \boldsymbol{x_i}) + b^* = 0, (其中(\boldsymbol{x_i}, y_i)为训练样本及对应标签)\]
分类决策函数为: \[f(x) = sign \big[\sum_{i=1}^m a_i^* y_i(\boldsymbol{x_i} \cdot \boldsymbol{x}) + b^* \big] \ \ \ (\boldsymbol{x} 为待预测样本)\]
线性可分支持向量机有且只有一个最优解, 具体证明见《统计学习方法》- 李航
2. 线性不可分SVM
2.1. 问题表示及拉格朗日函数
对每个样本点引入一个松弛变量\(\xi_i \geqslant 0\),使得线性不可分的点对应的支持超平面向着平行于其法线且朝着分离超平面的方向移动$ $作为伪支撑超平面上为参照(该点在此伪支撑超平面上), 使得函数距离约束变松。同时对松弛因子加入惩罚系数(超参数C, C > 0)。以上被称为软件个最大化,数学描述为:
\[\left\{ \begin{aligned} obj: \ & \min_{\boldsymbol{w},b,\boldsymbol{\xi}} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + C \sum_{i=1}^m \xi_i, \ C \geqslant 0 , & i\in[1, m] & \\ st: \ & y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b)\geqslant 1 - \xi_i, & i\in[1, m]& \\ & \xi_i \geqslant 0 , &\ i\in[1, m]& \\ & 满足y_0(\boldsymbol{w}^T\boldsymbol{x_0} + b) = 1 的点为支撑向量 & \end{aligned} \right. \tag{2.1} \]
为松弛变量\(\boldsymbol{\xi}\)引入拉格朗日乘子\(\boldsymbol{\mu}\),其拉格朗日函数为: \[ \begin{aligned} & L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu}) \\ = & \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + C \sum_{i=1}^m \xi_i + \sum_{i=1}^m \alpha_i \big[ 1 - \xi_i - y_i(\boldsymbol{w}^T\boldsymbol{x_i} + b) \big] - \sum_{i=1}^m \mu_i \xi_i \end{aligned} \]
2.2. KKT条件
\[\left\{ \begin{aligned} & \nabla_{\boldsymbol{w}} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu})\ = \boldsymbol{0} \Longrightarrow w^* - \sum_{i=1}^m \alpha_i^* y_i x_i =0 & \ \ \ \ (1)\\ & \nabla_{b} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu}) = 0 \Longrightarrow -\sum_{i=1}^m a_i^* y_i = 0 & \ \ \ \ (2) \\ & \nabla_{\xi_i} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu}) = 0 \Longrightarrow C - a^*_i - u^*_i = 0 \ & i\in[1, m] \ \ \ \ (3) &\\ & y_i(\boldsymbol{w^*} \cdot \boldsymbol{x_i} + b^*)\geqslant 1 - \xi_i^*, & i\in[1, m] \ \ \ \ (4)& \\ & \xi_i^* \geqslant 0 , &\ i\in[1, m] \ \ \ \ (5)& \\ & \alpha_i^* \geqslant 0 , &\ i\in[1, m] \ \ \ \ (6) & \\ & \mu_i^* \geqslant 0 , &\ i\in[1, m] \ \ \ \ (7) & \\ & \alpha_i^* \big[ 1 - \xi_i^* - y_i(\boldsymbol{w^*} \cdot \boldsymbol{x_i} + b^*) \big] = 0 , &\ i\in[1, m] \ \ \ \ (8)& \\ & \mu_i^* \xi_i^* = 0 , &\ i\in[1, m] \ \ \ \ (9) & \\ \end{aligned} \tag{2.2} \right. \]
2.3. 求解
2.3.1. \(\min_{\boldsymbol{w}, b, \boldsymbol{\xi}} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu})\)的求解
将(1),(2),(3)带入拉格朗日函数得, \[ \begin{aligned} & \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu}) \\ = & - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_j(\boldsymbol{x_i} \cdot \boldsymbol{x_j}) + \sum_{i=1}^m \alpha_i \end{aligned} \]
2.3.2. \(\max_{\boldsymbol{\alpha}, \boldsymbol{\mu}} \min_{\boldsymbol{w}, b, \boldsymbol{\xi}} L(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu})\)
考虑对偶问题最大化时求\(\boldsymbol{\alpha}\) 考虑KKT条件对上式有约束的条件: 由(3),(5),(7)消去\(\mu_i\)得: \[0 \leqslant \alpha_i \leqslant C\]
则, 对偶函数的可以表示为 \[ \begin{aligned} & \max_\boldsymbol{\alpha} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \\ = & \left\{ \begin{aligned} obj\ :\ &\max_{\boldsymbol{\alpha}} -\frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_j(\boldsymbol{x_i} \cdot \boldsymbol{x_j}) + \sum_{i=1}^m \alpha_i, \ \ \ \ i,j \in [1,\ldots, m]\\ st\ :\ &\ \sum_{i=1}^m \alpha^* y_i = 0,i \in [1,\ldots, m] \\ &\ 0 \leqslant \alpha_i \leqslant C, i \in [1,\ldots, m] \end{aligned} \right. \end{aligned} \]
用SMO求得\(\boldsymbol{\alpha}\),对于 \(0 < a_i < C\) 的样本点: 假设满足\(0 < a_i < C\)的个数为n
\[b^j = y_j - \sum_{i=i}^m \alpha_i ^ * y_i(\boldsymbol{x_i} \cdot \boldsymbol{x_j}),j \in [1, n]\] 实际求解过程中\[b^*=\frac{1}{n} \sum_{j=1}^n b^j\]
分离超平面为: \[\sum_{i=1}^m a_i^* y_i(\boldsymbol{x} \cdot \boldsymbol{x_i}) + b^* = 0, (其中(\boldsymbol{x_i}, y_i)为训练样本及对应标签)\]
分类决策函数为: \[f(x) = sign \big[\sum_{i=1}^m a_i^* y_i(\boldsymbol{x_i} \cdot \boldsymbol{x}) + b^* \big] \ \ \ (\boldsymbol{x} 为待预测样本)\]
超参数\(C\)为正则化常数,\(C\)越大, 分离超平面和支持超平面越距离越近, 训练集的准确率越高, 模型泛化能里越弱 当惩罚系数\(C \to +\infty\) 时,退化为线性可分的情况
拉格朗日乘子、松弛因子与支撑向量之间的关系:
- 当\(\alpha_i^* = 0\)时:非支持向量
- 当\(\alpha_i^* = C\)时:支持向量
- 当\(\xi_i^* > 1\)时: \(x_i\)为误分类点
- 当\(\xi_i^* = 1\)时: \(x_i\)为在分隔超平面上
- 当\(0 < \xi^* < 1\)时: \(x_i\)在分隔超平面和正确支撑超平面之间
- 当\(\xi^* = 0\)时:\(x_i\)是支撑超平面上的支持向量
- 当\(\xi_i^* > 1\)时: \(x_i\)为误分类点
- \(0 < \alpha_i^* < C\): \(x_i\)式支撑超平面上的支持向量。根据KKT条件\(C - a_i^* - u_i^* = 0\),此时\(u_i^* > 0\), 另有KKT条件\(u_i^*\xi_i^* = 0\),可得\(\xi_i^*=0\),即样本\(\boldsymbol{x_i}\)在支撑超平面上
2.3.3. 非线性不可分SVM
2.3.3.1. 问题求解
对于线性不可分的情况,使用核函数将原特征映射到更高维度后进行分类
核函数表示为 \(\kappa(x, z) = \varphi(x) \cdot \varphi(z)\),其中\(\varphi(x)\) 为某种映射函数
对于线性不可分的情况
\[
\begin{aligned}
& \max_\boldsymbol{\alpha} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) \\
= & \left\{
\begin{aligned}
obj\ :\ &\max_{\boldsymbol{\alpha}} -\frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m \alpha_i \alpha_j y_i y_j \kappa(\boldsymbol{x_i}, \boldsymbol{x_j}) + \sum_{i=1}^m \alpha_i, \ \ \ \ i,j \in [1,\ldots, m]\\
st\ :\ &\ \sum_{i=1}^m \alpha^* y_i = 0,i \in [1,\ldots, m] \\
&\ 0 \leqslant \alpha_i \leqslant C, i \in [1,\ldots, m]
\end{aligned}
\right.
\end{aligned}
\]
求得\(a_i^*\)后
\[b^* = \frac{1}{n} \sum_{j=1}^n \big[y_j - \sum_{i=i}^m \alpha_i ^ * y_i \kappa(\boldsymbol{x_i}, \boldsymbol{x_j}) \big], 0 < a_j < C\]
分离超平面为:
\[\sum_{i=1}^m a_i^* y_i \kappa(\boldsymbol{x_i}, \boldsymbol{x_j}) + b^* = 0, (其中(\boldsymbol{x_i}, y_i)为训练样本及对应标签)\]
分类决策函数为:
\[f(x) = sign \big[\sum_{i=1}^m a_i^* y_i \kappa(\boldsymbol{x_i}, \boldsymbol{x}) + b^* \big] \ \ \ (\boldsymbol{x} 为待预测样本)\]
2.3.4. 核函数
以下x,z为向量
线性核
\[\kappa(x, z) = x \cdot z\]多项式核
\[\kappa(x, z) = (\gamma x \cdot z + r)^p\]rbf核(高斯核)
\[\kappa(x, z) = exp \big(-\frac{\lVert x - z\rVert^2 }{2 \sigma^2}\big)\]双曲正切核(sigmoid核) \[\kappa(x, z) = tanh(\gamma x \cdot z + r)\]
更多核函数见机器学习核函数手册
3. SMO
Sequential minimal optimization
序列最小优化算法,https://en.wikipedia.org/wiki/Sequential_minimal_optimization
详见《统计学习方法》,李航著,\(P_{124}\)
4. 损失函数
考虑约束问题式(2.1),将不等式约束部分和约束整合,可以得到线性支持向量机的损失为hinge损失,形式如下: \[\sum_{i=1}^m \max \left\{ 0, 1 - (\boldsymbol{w}^T x_i + b) y_i \right\}\]
当随时函数点样本点到正确分类的超平面的集合距离小于1时, 有损失, 损失为该点到对应正确分类支撑超平面的函数距离.即: + 对于正例(\(y_i = 1\)): 正支撑超平面的下方样本点有损失, hinge损失为点到正支撑超平面的函数距离 + 对于负例(\(y_i = -1\)): 负支撑超平面的上方样本点有损失, hinge损失为点到负支撑超平面的函数距离
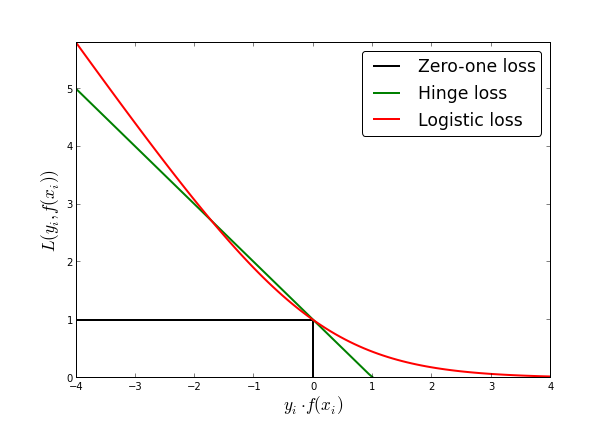
hige核心在于只关心核心点(支持向量)造成的损失,且这部分损失是线性的(区别与0-1损失),放弃一定范围外且正确分类点(区别于logistic损失)
hinge损失 + L2正则的最小化问题等价为线性支持向量机的最优化问题.即支持向量最优化问题可以表示为如下:
\[ \min\limits_{\boldsymbol{w}, b} \left[ \sum_{i=1}^m \max \left\{ 0, 1 - (\boldsymbol{w}^T x_i + b) y_i \right\} + \lambda \lVert \boldsymbol{w} \rVert^2 \right] \] \[\lambda=\frac{1}{2C},\ C > 0\]
从hinge损失的角度考虑,因为全局不可导,所以可以用随机梯度下降的来求参数: 为方便推导, 每个样本扩充一个常数1, 则有\(x_i \to (x_i, 1)^T\), 则 \(\boldsymbol{w}^T x_i + b \to \boldsymbol{w}^T x_i\)
\[ \nabla_\boldsymbol{w} = \left\{ \begin{aligned} & 2 \lambda \boldsymbol{w} - \boldsymbol{x_i} y_i &,& if \ \ \boldsymbol{w}^T \boldsymbol{x_i} < 1 \\ & 2 \lambda \boldsymbol{w}& , &other \\ \end{aligned} \right. \]
则学习率为第t次步长\(\eta_t\)的随机梯度下降算法为: \[ \boldsymbol{w_{t+1}} = \left\{ \begin{aligned} & \boldsymbol{w_t} - \eta_t (2 \lambda \boldsymbol{w_t} - \boldsymbol{x_i} y_i) &,& if \ \ \boldsymbol{w}^T \boldsymbol{x_i} < 1 \\ & \boldsymbol{w_t} - \eta_t (2 \lambda \boldsymbol{w_t})& ,& other \\ \end{aligned} \right. \]
对于SVM在只关注核心点的同时, 选择分离超平面的原则使得熵最大, 即使得两支撑超平面到分离超平面的距离相等,保证了其泛化能力, 比较适合稀疏样本分类。 但如果支持向量是个噪声点的话会对结果有较大的影响, 可以通过降低原约束问题的\(C\)降低对噪声点的敏感程度
5. SVM与感知机异同
感知机是误分类点算法驱动的, 其损失函数: \[\sum_{i=1}^m \max \left\{ 0, - (\boldsymbol{w}^T \boldsymbol{x_i} + b) y_i \right\}\]
最优化问题可以表示为 \[ \min\limits_{\boldsymbol{w}, b} \left[ \sum_{i=1}^m \max \left\{ 0, - (\boldsymbol{w}^T \boldsymbol{x_i} + b) y_i \right\} \right] \]
对比SVM的hinge + L2-norm, 可以看到SVM比感知机加了正确分类但函数间隔小于1的惩罚 ,并且假如L2-norm项
由于感知机对所有分类正确的点都没有惩罚, 所以即使线性可分的情况下,感知机模型也不是唯一的.感知机参数可以用随机梯度下降方法训练得到, 每次选择当前参数下误分类样本用于训练
6. 概率化的结果输出
考虑二分类问题, 对于样本类别\({+1, -1}\), 假设待预测样本的为\(+1\)概率\(p = \frac{1}{1+exp^{-\phi(x)}}\),则其为\(-1\)的概率为1 - p, 则有 \(ln(\frac{p}{1-p}) = \phi(x)\), \(\phi(x)\)发生与不发生的概率比取对数, 被称为对数几率比
\[\left\{ \begin{aligned} & \frac{p}{1-p} > 1 \Rightarrow \phi(x) > 0: \ \ & 认为样本类别为 +1 \\ & \frac{p}{1-p} < 1 \Rightarrow \phi(x) < 0: \ \ & 认为样本类别为 -1 \\ \end{aligned} \right. \tag{6.1} \]
对于SVM,假设训练好参数\(\boldsymbol{w}\), \(b\). 令\(f(x) = \boldsymbol{w} \cdot \boldsymbol{x} + b\), 则有 \[\left\{ \begin{aligned} & f(x) > 0:&认为样本类别为 +1 \\ & f(x) < 0:&认为样本类别为 -1 \\ \end{aligned} \right. \tag{6.2} \]
\[\left\{ \begin{aligned} & f(x) > 0:&认为样本类别为 +1 \\ & f(x) < 0:&认为样本类别为 -1 \\ \end{aligned} \right. \tag{6.2} \]
对比(6.1),(6.2)可以看出SVM的函数距离和对数几率比对预测结果有类似,所以假设SVM的函数距离的线性函数是某种对数几率比:即认为\(\phi(x) = -\big[af(x) + b \big]\), 最终概率 \[p = \frac{1}{1+exp^{f(x)}}\] 其中\(a\), \(b\)通过极大似然估计,在mlapp中特别说明如果用原来数据集求解\(a\),\(b\)容易过拟合, 建议用单独数据集训练
其极大似然为: \[L=\prod_{i=1}^m \big[\frac{1}{1+exp^{af(x_i) + b}}\big]^\frac{y_i+1}{2} \cdot \big[\frac{af(x_i) + b}{1+exp^{af(x_i) + b}}\big]^ {-\frac{y_i - 1}{2}}\]
对数极大似然问题为: \[l(a, b) =\sum_{i=1}^m \Bigg[\frac{y_i+1}{2} \frac{1}{1+exp^{af(x_i) + b}} -\frac{y_i - 1}{2} \frac{af(x_i) + b}{1+exp^{af(x_i) + b}}\Bigg]\]
所以问题的解如下: \[\arg \min_{a, b}-l(a, b)\]
可以通过梯度下降或拟牛顿等方法求得a, b
Platt还提出把标签分别把正负例的y_i转化为和其类别样本数相关的概率数,转化方法见https://en.wikipedia.org/wiki/Platt_scaling
! 但是mlapp中指出验证效果并不理想, 同时相关向量机(Relevance Vector Machine)可以较好的拟合概率
7. 多分类SVM
7.1. 直接公式法
https://www.csie.ntu.edu.tw/~cjlin/papers/multisvm.pdf
7.2. 一对剩余(One Versus Rest, OVR)
把其中一个类别做为\(+1\)类, 其他类别做为\(-1\)类, 训练K个二分SVM,选择 \(y_i(\boldsymbol{w}^T x_i + b)\)的最大的对应的距离, 因为是一对多的情况所以不平衡样本的问题突出,可以通过正例重采样,Lee et al. (2001) 提出修改负例的标签为\(-\frac{1}{k-1}\),因为不是在同一参考下生成的模型,所以通过直接找出函数距离最大的作为最终分类可信度受限。
7.3. 一对剩余(One Versus One, OVO)
一次拿出两类训练分类器, k类一共有\(\frac{k(k-1)}{2}\)个分类器,对每个样本的类别结果做统计,众数对应的类别为最后对应的类别
8. SVR
http://reset.pub/2017/03/26/svr
9. sklearn中的SVM
http://scikit-learn.org/stable/modules/svm.html#svm
SVC:
http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC
http://scikit-learn.org/stable/modules/generated/sklearn.svm.NuSVC.html#sklearn.svm.NuSVC
SVR:
http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html#sklearn.svm.SVR
|
|
分类问题中,针对不平衡样本, 通过class_weight参数,达到提高少数样本的召回率
10. 参考资料
[1]《统计学习方法》,李航著,2012
[2]《机器学习》,周志华著,2016
[3]《Machine Learning - A Probabilistic Perspective》,Kevin P. Murphy ,2012
[4]《Pattern Recognition And Machine Learning》,Christopher Bishop,2007
[5] 维基百科-支持向量机:https://zh.wikipedia.org/wiki/支持向量机
[6] 随机梯度求SVM http://ttic.uchicago.edu/~nati/Publications/PegasosMPB.pdf
[7] 多分类SVM:https://www.csie.ntu.edu.tw/~cjlin/papers/multisvm.pdf
[8] 多分类SVM:[!PDF] Multi-Class Support Vector Machine - Springer
[9] PRML翻译:https://mqshen.gitbooks.io/prml/
[10] 机器学习核函数手册:https://my.oschina.net/lfxu/blog/478928
[11] sklearn-核函数:http://scikit-learn.org/stable/modules/svm.html#svm-kernels
[12] 支持向量回归:http://blog.jasonding.top/2015/05/01/Machine%20Learning/【机器学习基础】支持向量回归
[13] SVM等于Hinge损失 + L2正则化:http://breezedeus.github.io/2015/07/12/breezedeus-svm-is-hingeloss-with-l2regularization.html
[14] 维基百科-Platt_scaling: https://en.wikipedia.org/wiki/Platt_scaling
[15] sklearn-svm:http://scikit-learn.org/stable/modules/svm.html#svm