SVR,Support Vector Regression,支持向量回归
1. SVR问题引出
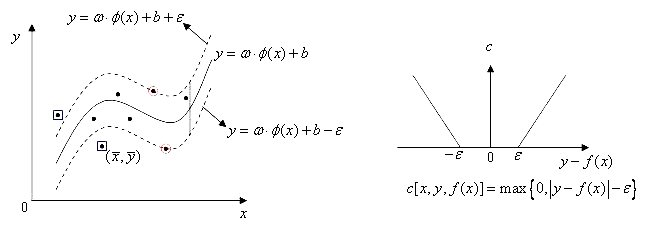
有样本集 \(D=\{(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),\ldots,(\boldsymbol{x_m},y_m)\}\)。其中, \(\boldsymbol{x_i}\)是一个样本,列向量;\(y_i\)为回归目标,\(y_i \in \mathbb{R}\)。 找到一个回归模型\(f(x) = \boldsymbol{w}^T\boldsymbol{x} + b\),使得\(f(\boldsymbol{x})\)与\(y\)在损失为\(\epsilon\)不敏感损失下尽可能接近,其中回归线由落在\(\boldsymbol{w} \cdot \boldsymbol{x} + b - \epsilon = 0\)与\(\boldsymbol{w} \cdot \boldsymbol{x} + b + \epsilon = 0\)区域内的点参与构建
2. 数学表达
假设样本结果为y, 预测结果为\(\widehat{y}\),定义\(\epsilon\)不敏感损失为: \[
L_\epsilon(y, \widehat{y}) =
\left\{
\begin{aligned}
& 0 & if \ \ & \lvert y - \widehat{y} \rvert < \epsilon \\
& \lvert y - \widehat{y} \rvert - \epsilon & & otherwise
\end{aligned}
\right. \tag{1}
\]
上式 \(\epsilon > 0\),epsilon的意义:在离回归线上下\(\epsilon\)都不计入损失,其回归线可以看成回归线上下\(\epsilon\)区域边界组成的回归带,落在在回归带上的点x损失为0,预测\(\widehat{y}\)为固定x后回归带的中点
误差为epsilon不敏感,使用L2正则的模型为: \[J = C \sum_{i=1}^m L_\epsilon(y, \widehat{y}) + \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 \tag{2}\]
2.1. \(2\epsilon\)回归带能够覆盖所有点的情况
对于固定的\(\epsilon\),所有点均在回归带上的情况: \[ \left\{ \begin{aligned} obj\ :\ \ & \min_{\boldsymbol{w},b,\epsilon} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 \\ st\ :\ \ & \lvert f(\boldsymbol{x_i})- y_i \rvert \leqslant \epsilon \end{aligned} \right. \tag{3} \]
2.2. \(2\epsilon\)回归带不能够覆盖所有点的情况
参照SVM的线性不可分的情况,为每个样本引入松弛因子\(\xi_i\)使得不在回归带的点满足约束,并且在目标函数中加入对松弛因子的惩罚项\(C\),则有
\[ \left\{ \begin{aligned} obj\ :\ \ & \min_{\boldsymbol{w},b,\epsilon} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + C \xi_i \\ st\ :\ \ & \lvert f(\boldsymbol{x_i}) - y_i \rvert \leqslant \epsilon + \xi_i \\ & \xi_i \geqslant 0 \end{aligned} \right. \tag{4} \]
3. 问题求解
3.1. 将转化为凸优化问题
考虑上式约束不连续可导,分情况去掉绝对值: \[ \begin{eqnarray} 隔离带上方的样本:& f(x_i) & & & < & y_i < f(x_i) + \epsilon + \xi^+_i \\ 隔离带下方的样本:& f(x_i) & - \epsilon & - \xi^-_i & < & y_i < f(x_i) \\ 隔离带上的样本: & f(x_i) & - \epsilon & & \leqslant & y_i \leqslant f(x_i) + \epsilon \end{eqnarray} \tag{5} \]
综上约束条件可以化为:
\[
f(x_i) - \epsilon - \xi^-_i \leqslant y_i \leqslant f(x_i) + \epsilon + \xi^+_i
\] \(\xi^-_i \geqslant 0, \xi^+_i \geqslant 0\)。如果要求上下界是紧的,松弛因子至多有一个不为0,即\(\xi^-_i \xi^+_i=0\)
式(4)中将\(f(x) = \boldsymbol{w} \cdot \boldsymbol{x} + b\),替换等价约束可以转化为: \[
\left.
\begin{aligned}
obj\ :\ \ & \min_{\boldsymbol{w},b,\boldsymbol{\xi}} \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + C\sum_{i=1}^m(\xi^+_i + \xi^-_i ) \\
st\ :\ \ & \boldsymbol{w} \cdot \boldsymbol{x_i} + b - \epsilon - \xi^-_i - y_i \leqslant 0\\
& y_i - \boldsymbol{w} \cdot \boldsymbol{x_i} - b - \epsilon - \xi^+_i \leqslant 0 \\
& -\xi^+_i \leqslant 0 \\
& -\xi^-_i \leqslant 0 \\
& C,\epsilon 为超参数,C >0,\epsilon \geqslant 0
\end{aligned}
\right. \tag{6}
\]
对于一个样本点\(x_i\)其松弛因子\(\xi^+_i\)和\(\xi^-_i\)至多只有一个大于0
式(6)为不带等式约束的凸优化
3.2. 拉格朗日函数
引入拉格朗日乘子\(\alpha_i^+ \geqslant 0\), \(\alpha_i^- \geqslant 0\),\(\mu^+_i \geqslant 0\)和\(\mu^-_i \geqslant 0\),则拉格朗日函数为: \[ \begin{aligned} L(\boldsymbol{w},b,\boldsymbol{\xi^+},\boldsymbol{\xi^-},\boldsymbol{\alpha^+}, \boldsymbol{\alpha^-},\boldsymbol{\mu^+},\boldsymbol{\mu^-})= & \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 + C\sum_{i=1}^m(\xi^+_i + \xi^-_i ) \\ & + \sum_{i=1}^m \alpha_i^-(\boldsymbol{w} \cdot \boldsymbol{x_i} + b - \epsilon - \xi^-_i - y_i)\\ & + \sum_{i=1}^m \alpha_i^+(y_i - \boldsymbol{w} \cdot \boldsymbol{x_i} - b - \epsilon - \xi^+_i ) \\ & - \sum_{i=1}^m \mu_i^+ \xi_i^+ \\ & - \sum_{i=1}^m \mu_i^- \xi_i^- \end{aligned} \tag{7} \]
3.3. 拉格朗日对偶函数
3.3.1. 拉格朗日函数极小问题
则,\(L(\boldsymbol{w},b,\boldsymbol{\xi^+},\boldsymbol{\xi^-})\)取最极小值时满足(KKT条件之一),以下公式均为取得最优值满足的条件,例:\(\boldsymbol{w}\) 实际表示 \(\boldsymbol{w^*}\),可参考SVM: \[ \left\{ \begin{eqnarray} & \nabla_{\boldsymbol{w}}L = 0 & \Longrightarrow & \boldsymbol{w} + \sum_{i=1}^m a_i^- \boldsymbol{x_i} - \sum_{i=1}^m \alpha_i^+ \boldsymbol{x_i} = 0 \ \ \ & (1) \\ & \nabla_{\boldsymbol{b}}L = 0 & \Longrightarrow & \sum_{i=1}^m \alpha_i^+ - \sum_{i=1}^m a_i^- = 0 & (2)\\ & \nabla_{\boldsymbol{\xi_i^+}}L = 0 & \Longrightarrow & C - \alpha_i^+ - \mu_i^+ = 0 & (3) \\ & \nabla_{\boldsymbol{\xi_i^-}}L = 0 & \Longrightarrow & C - \alpha_i^- - \mu_i^- = 0 & (4)\\ \end{eqnarray} \tag{8} \right. \]
整理上式得: \[ \begin{aligned} L = & \frac{1}{2}\lVert\boldsymbol{w}\rVert^2 +\boldsymbol{w} \sum_{i=1}^m(a_i^- \boldsymbol{x_i} + a_i^+ \boldsymbol{x_i}) \\ & + (C - a_i^+ - u_i^+)\sum_{i=1}^m \xi_i^+ \\ & + (C - a_i^- - u_i^-)\sum_{i=1}^m \xi_i^- \\ & + b\sum_{i=1}^m(a_i^- - a_i^+) \\ & - \epsilon\sum_{i=1}^m (a_i^- + a_i^+) \\ & - \sum_{i=1}^m y_i(a_i^- - a_i^+) \\ \end{aligned} \tag{9} \]
将式(8)带入拉格朗日函数得拉格朗日对偶函数为:
\[ \begin{aligned} \max_{\boldsymbol{a^+},\boldsymbol{a^-}}L = & -\frac{1}{2}\lVert\boldsymbol{w}\rVert^2 - \epsilon\sum_{i=1}^m (a_i^- + a_i^+) - y_i \sum_{i=1}^m(a_i^- - a_i^+) \\ = & -\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m(a_i^- - a_i^+)(a_j^- - a_j^+)\boldsymbol{x}_i \cdot \boldsymbol{x}_j \\ & - \epsilon\sum_{i=1}^m (a_i^- + a_i^+) - y_i \sum_{i=1}^m(a_i^- - a_i^+) \end{aligned} \tag{10} \]
3.3.2. 拉格朗日极大极小问题
考虑除(8)以外的KKT条件: \[ \left\{\ \ \ \begin{aligned} & \alpha_i^-(\boldsymbol{w} \cdot \boldsymbol{x_i} + b - \epsilon - \xi^-_i - y_i) = 0 & \ \ & (1) \\ & \alpha_i^+(y_i - \boldsymbol{w} \cdot \boldsymbol{x_i} - b - \epsilon - \xi^+_i ) = 0 & & (2) \\ & \mu_i^+ \xi_i^+ = 0 & &(3)\\ & \mu_i^- \xi_i^- = 0 & &(4) \\ & \boldsymbol{w} \cdot \boldsymbol{x_i} + b - \epsilon - \xi^-_i - y_i \leqslant 0 & &(5) \\ & y_i - \boldsymbol{w} \cdot \boldsymbol{x_i} - b - \epsilon - \xi^+_i \leqslant 0 & & (6) \\ & -\xi^+_i \leqslant 0 & & (7) \\ & -\xi^-_i \leqslant 0 & & (8) \\ & \alpha_i^+,\alpha_i^-,\mu^+_i ,\mu^-_i \geqslant 0 & & (9) \\ \end{aligned} \tag{11} \right. \]
3.3.3. \(\alpha_i^+\)与\(a_i^-\)约束关系
\(\sum_{i=1}^m(\alpha_i^+ - \alpha_i^- )= 0\)
式(8).2\(0 \leqslant \alpha_i^+ ,\alpha_i^- \leqslant C\)
证明:
\[ \left. \begin{aligned} 式(8).3:& \ \ C - \alpha_i^+ - \mu_i^+ = 0 \\ (11).9:& \ \ \mu_i^+ \geqslant 0, \alpha_i^+ \geqslant 0 \end{aligned} \right\} \Longrightarrow 0 \leqslant \alpha_i^+ \leqslant C \\ \\ 同理:0 \leqslant \alpha_i^- \leqslant C \]\(\alpha_i^+ \alpha_i^- = 0\)
证明: 假设\(\alpha_i^+ > 0\),\(\alpha_i^- > 0\),则根据式(11)中的1,2,5,6可得 \[ \begin{aligned} \boldsymbol{w} \cdot \boldsymbol{x_i} + b - \epsilon - \xi^-_i - y_i = 0 & \ \ &(1)\\ y_i - \boldsymbol{w} \cdot \boldsymbol{x_i} - b - \epsilon - \xi^+_i = 0 & &(2) \end{aligned} \tag{13} \] 以上两式相加可得:\(-2 \epsilon = \xi_i^+ + \xi_i^-\),与约束\(\epsilon > 0,\xi_i^+ \leqslant 0, \xi_i^- \leqslant 0\)相违背。 则证明\(\alpha_i^+\)和\(\alpha_i^-\)至少有一个等于0,即\(\alpha_i^+ \alpha_i^- = 0\)得证
3.3.4. 考虑约束项的拉格朗日对偶问题
\[ \left\{ \begin{aligned} obj : & \left. \begin{aligned} \max_{\boldsymbol{a^+},\boldsymbol{a^-}} \ \ & -\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m(a_i^- - a_i^+)(a_j^- - a_j^+)\boldsymbol{x}_i \cdot \boldsymbol{x}_j \\ & - \epsilon\sum_{i=1}^m (a_i^- + a_i^+) - y_i \sum_{i=1}^m(a_i^- - a_i^+) & \end{aligned} \right. \\ st :& \sum_{i=1}^m (\alpha_i^+ - a_i^-) = 0 \\ & 0 \leqslant \alpha_i^+, \alpha_i^- \leqslant C \\ & \alpha_i^+ \alpha_i^- = 0 \end{aligned} \right. \tag{14} \]
3.4. 拉格朗日乘子、松弛因子、支持向量的关系
- \(\xi_i^+ \xi_i^- = 0\)
一个样本的松弛因子最多只有一个不为0
考虑以下KKT条件:
\[
\left\{
\begin{aligned}
式(8).3:& C - \alpha_i^+ - \mu_i^+ = 0 \\
式(11).3:& \mu_i^+ \xi_i^+ = 0 \\
式(12).2:& 0 \leqslant \alpha_i^+ \leqslant C \\
\end{aligned}
\right.
\]
则可以得出以下结论:
- 当\(\alpha_i^+ = C\)时: \(\alpha_i^- = 0,\mu_i^+ = 0,\xi_i^+ > 0\),样本点在epsilon回归带之外,且在回归带上方
- 当0 < \(\alpha_i^+ < C\)时: \(\alpha_i^- = 0,\mu_i^+ > 0, \xi_i^+ = 0\),样本点在回归线及上epsilon回归带中间,为支持向量
- 当\(\alpha_i^+ = 0\)时: \(\mu_i^+ > 0,\xi_i^+ = 0\),样本点在回归线及上epsilon回归带中间
同理
- 当\(\alpha_i^- = C\)时: \(\alpha_i^+ = 0,\mu_i^- = 0,\xi_i^- > 0\),样本点在epsilon回归带之外,且在回归带下方
- 当0 < \(\alpha_i^- < C\)时: \(\alpha_i^+ = 0,\mu_i^- > 0, \xi_i^- = 0\),样本点在回归线及下epsilon回归带中间,为支持向量
- 当\(\alpha_i^- = 0\)时: \(\mu_i^- > 0,\xi_i^- = 0\),样本点在回归线及下epsilon回归带中间
考虑式(8).2 可以得到回归直线为: \[f(x) = \sum_{i=1}^m(a_i^+ - a_i^-)\boldsymbol{x_i} \cdot \boldsymbol{x} + b^* \tag{15}\]
满足\(a_i^+ - a_i^- \neq 0\)对应的点\(\boldsymbol{x_i}\)为支持向量
3.5. \(b^*\)的求解
当 \(0 \leqslant a_j^+ \leqslant C\)时,\(a_j^- = 0\),由式(13).1可得
\[ b^*=-\sum_{i=1}^m(a_i^+ - a_i^-)\boldsymbol{x_i} \cdot \boldsymbol{x_j}+ \epsilon + y_j \]
当 \(0 \leqslant a_j^- \leqslant C\)时,\(a_j^+ = 0\),由式(13).2可得
\[ b^*=-\sum_{i=1}^m(a_i^+ - a_i^-)\boldsymbol{x_i} \cdot \boldsymbol{x_j} - \epsilon + y_j \]
考虑当\(0 \leqslant a_j^+ \leqslant C\)时,\(a_j^- = 0\),由式(13).1,当\(0 \leqslant a_j^- \leqslant C\)时,\(a_j^+ = 0\),由式(13).2可得 \[ b^* = \left\{ \begin{aligned} &-\sum_{i=1}^m(a_i^+ - a_i^-)\boldsymbol{x_i} \cdot \boldsymbol{x_j}+ \epsilon + y_j,0 \leqslant a_j^+ \leqslant C \\ &-\sum_{i=1}^m(a_i^+ - a_i^-)\boldsymbol{x_i} \cdot \boldsymbol{x_j} - \epsilon + y_j,0 \leqslant a_j^- \leqslant C \end{aligned} \right. \]
4. 引入核函数.
\(\kappa(\boldsymbol{x}, \boldsymbol{z}) = \varphi( \boldsymbol{x}) \cdot \varphi( \boldsymbol{z})\)替换以上\(\boldsymbol{x} \cdot \boldsymbol{z}\)形式 则: \[f(x) = \sum_{i=1}^m(a_i^+ - a_i^-)\kappa(\boldsymbol{x_i}, \boldsymbol{x}) + b^*\]
\[ b^* = \left\{ \begin{aligned} &-\sum_{i=1}^m(a_i^+ - a_i^-) \kappa(\boldsymbol{x_i}, \boldsymbol{x_j}) + \epsilon + y_j,0 \leqslant a_j^+ \leqslant C \\ &-\sum_{i=1}^m(a_i^+ - a_i^-) \kappa(\boldsymbol{x_i}, \boldsymbol{x_j}) - \epsilon + y_j,0 \leqslant a_j^- \leqslant C \end{aligned} \right. \]
5. 参考资料
[1]《机器学习》,周志华著,2016
[2]《Machine Learning - A Probabilistic Perspective》,Kevin P. Murphy ,2012
[3]《Pattern Recognition And Machine Learning》,Christopher Bishop,2007
[4] 支持向量回归:http://blog.jasonding.top/2015/05/01/Machine%20Learning/【机器学习基础】支持向量回归